|
2000年开始,深圳东部地区除了已经存在的盐田港和大亚湾的扩建, 陆续进行了龙岗大工业区,坪山工业区的兴建, 龙岗中心城的建设,东海岸商业住宅的开发.这条隧道是进出深圳东部的“华山一条路”,垄断了市区和东部之间的交通。而每次10-30元隧道收费的直接后果,不但造成经常性堵车,更是抬高了在东部居住和企业经营的成本,成为盐田区经济发展的交通瓶颈和企业投资决策的不利因素。项目管理者联盟
从1996-2002年,每年的市区“两会”上,梧桐山隧道收费都要受到人大代表的质疑。 深圳市政府与盐田港及达佳集团进行了 7 次的正式谈判, 与梧桐山隧道公司进行了多达38 次谈判, 并一度接近达成协议, 但各种方案最终都被搁置。项目管理者联盟
2004年,深圳市政府提出以9亿元的价格收购梧桐山隧道,但是梧桐山隧道公司的要价是13亿,其中10亿元须一次性支付。最终因要价太高双方未能达成协议。项目管理者联盟
2-3. 开通两路与收购协议项目管理者联盟
为了解决深圳东部地区发展的交通运输瓶径,深圳市政府在2002年12月斥资1.18亿元改造并重新开通了梧桐山盘山公路,2008年7月,投资约27.64亿元的深盐二通道正式通车,两条道路完全免费,东部地区交通运输的瓶径问题获得了彻底的解决.项目管理者联盟
深盐二通道开通后,梧桐山隧道的车流量立刻下降。后来梧桐山隧道一年收入只有3000万,只够人员养护略有结余,大约只有300多万的利润。二通道动工后港方的谈判价码从13个亿一直降到9个多亿,开通前又降到6.8亿,而政府根据二通道开通后的流量和剩余年限的的悲观估价在1.58亿,乐观估价在3.8亿.项目管理者联盟
盐田区政府的介入解决了最后收购的难点. 通过盐田港集团用5.5亿的价格收购隧道的股权,用2.5亿的价格卖给政府. 盐田区政府通过国土规划将隧道公司原来的土地划拨给盐田港集团,集团通过土地的商业开发获得3亿的收入.政府最终的收购代价是5.5亿.2011年2收购成功,3月隧道免费通车.项目管理者联盟
3. 博弈论与应用问题www.mypm.net
3-1 囚徒困境PD与纳什平衡NE问题项目管理者联盟
如果你百度 “PPP GAME THEORY”,可以看到16万网页文章.谷歌学术则可以搜索到2.4万文章.在众多的PPP文献中,中外学者都以政府与企业之间的搏弈和纳什平衡来作为理论基础.在这个理论中,哲学上有名的囚徒困境被用来比喻政府企业合作中的博弈关系.(囚徒困境是著名的哲学范例,有很多不同的情节和细节描述.后面的描述以<斯坦福哲学百科全书>中情节的为例)项目管理者联盟
罪犯甲与罪犯乙被关进了公安局,两个人被分开审讯。检查官告诉罪犯甲,如果你招供,而罪犯乙不招供,你将被释放,而罪犯乙将被判刑十年;警察告诉罪犯乙,如果你招供,而罪犯甲不招供,你将被释放,而罪犯甲将被判刑十年;根据涉案金额,如果两人都招供了,均被判刑五年;根据案情和警方掌握的证据判断,如果两人都不招供,各自只能被判刑两年。项目管理者联盟
把上述例子中的罪犯甲和罪犯乙换成PPP中的政府和企业,各自站在自己的利益角度考虑问题和决策行为,就是政府与企业合作中的纳什平衡.项目经理圈子
 项目管理者联盟 项目管理者联盟
现代博弈论从50年德国数学家冯.纽曼和美国经济学家纳什提出之后, 很多学者针对初始的博弈论进行了不断深入研究,质疑批判和发展完善,进行了大量的社会实践的验证性实验,以至于初始的博弈论被称为经典博弈论以区别后续的各种博弈理论.当人们讨论和应用博弈论的时候,需要搞清楚是指的哪个博弈论.而在政府与企业的合作中,事情远远不是纳什平衡描述的那样简单.换句话说,囚徒困境PD和纳什平衡NE仅仅是种 “简单的和非典型”的博弈格局和平衡状态.bbs.mypm.net
在针对经典博弈论的理性批判,社会验证和发展完善中,受到质疑的几个主要问题恰恰是政府和企业在将博弈论应用到PPP合作中需要注意的问题.而错误的行动来自错误的思想理论或错误的应用对象.项目管理者联盟
下面针对政府企业PPP合作,结合梧桐山隧道项目案例,讨论博弈论应用到PPP政府与企业合作对象的三个主要问题:项目管理者联盟
1.(策略问题) PPP博弈具有多种平衡状态SPE,并不局限在纳什平衡NE项目管理者联盟文章
2.(定位问题) PPP博弈发生在集体理性与个体理性之间,而不是个体理性之间.项目管理者联盟
3.(参与者问题) PPP博弈的参与者是人性人,经济理性是人性的局部成分.项目管理者联盟
理性经济人是人群的部分人员.club.mypm.net
3-2 PPP博弈的解决方案具有多种平衡,并不局限在纳什平衡项目管理者联盟
很多博弈论学者提出囚徒困境和纳什平衡NE仅仅是现实生活中一个 “简易的和非典型的零和博弈”,属于封闭信息环境下的 “同步博弈”格局-Imperfect information and simultaneous move game.2006年赫维奇提出”机制设计”的思想, 并再次以博弈论为主题获得诺贝尔经济学奖.这种最佳的平衡被称为”子集的最佳平衡” SPE-Subgame perfect equilibrium. 以区别”纳什平衡NE-Nash Equilibrium, 见图(3). 即使是作为理性经济人(这是个暂时的让步,后续讨论理性经济人存在的问题), (4,5)是子集的最佳平衡解,图中的数字分别表示博弈双方的效用值高低.项目管理者联盟
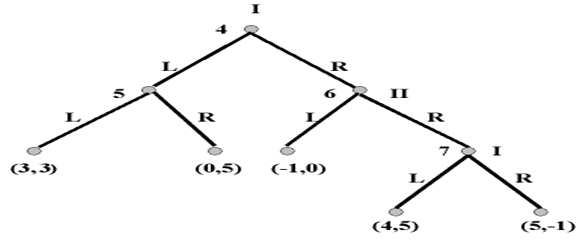 项目管理者联盟 项目管理者联盟
PPP实践人员需要注意的是,政府与企业PPP合作不是囚徒困境那样的封闭信息环境-防止串供环境, 坚实的法律基础,通明的合作程序,公开的信息披露是基本的信息环境.政府和企业都没有必要 “偷偷摸摸”和 “声东击西”.即使在局部问题上进入博弈状态, 政府与企业进入的是信息公开透明的讨价还价.这种博弈格局被称为透明信息下的顺序博弈-- perfect information and sequential move game.而纳什平衡NE不是这种格局的最佳解, 例如囚徒串供的博弈树如图(4), 囚徒2在知道囚徒1的策略后,可能选择(3,3)的对策,并获得最佳的解决方案.项目管理者联盟
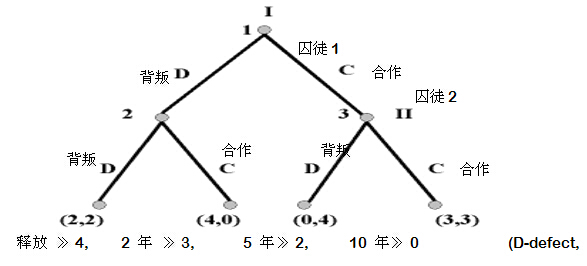 项目管理者联盟 项目管理者联盟
本文为项目管理者联盟联盟会员原创文章,授权发布,非经同意不得转载!
|








